Algoritmos O grande

Author

Luis Alberto Rodríguez Catana

Published

May 12, 2025

Versión corregida.

Introducción

El presente trabajo muestra los resultados obtenidos a partir de la simulación de los órdenes de crecimiento O(1) vs O(logn), O(n) vs O(nlogn), O(n2) vs O(n3), O(an) vs O(n!), O(n!) vs O(nn), propuestos para su simulación.

Con la finalidad de obtener un antecedente sobre cómo resolver este tipo de ejercicio se consultó lo relacionado con la notación O grande, la cual es una herramienta utilizada para describir el rendimiento o la complejidad temporal de un algoritmo en función del tamaño de la entrada.

El objetivo principal de la notación O grande de acuerdo con Bhargava, A., 2016, es evaluar cuán veloz es un algoritmo, expresando su eficiencia en términos de su comportamiento a medida que el tamaño de la entrada (n) crece. A continuación, se describen las notaciones más comunes de la notación O grande:

\(O(1)\): Tiempo constante
\(O(\log n)\): Tiempo logarítmico
\(O(n)\): Tiempo lineal
\(O(n \log n)\): Tiempo lineal-logarítmico
\(O(n^2)\): Tiempo cuadrático
\(O(2^n)\): Tiempo exponencial
\(O(n!)\): Tiempo factorial
\(O(n^n)\): Tiempo exponencial en base \(n\)

De acuerdo con lo anterior la notación O grande describe el comportamiento asintótico de una función, en esta primera práctica de experimentación se compararon distintos órdenes de crecimiento.

Definición de funciones de complejidad en Julia

El primer paso en el proceso consistió en definir funciones en Julia que simulan cada orden de crecimiento.

Se utilizaron las librerías

import Pkg; Pkg.add("DataFrames")

using Plots, DataFrames, Printf gr()

function Onlogn(n)
    return n * log(n)
end

# O(n^2) - Tiempo cuadrático
function On2(n)
    return n^2
end

# O(n^3) - Tiempo cúbico
function On3(n)
    return n^3
end

# O(a^n) - Tiempo exponencial (a > 1)
function Oan(n, a=2)
    return a^n
end

# O(n!) - Tiempo factorial
function Onfactorial(n)
    return factorial(n)
end

# O(n^n) - Tiempo exponencial en base n
function Onn(n)
    return n^n
end

# Rangos adecuados para cada comparación
n_values = 1:100  # Para O(1) vs O(log n) y O(n) vs O(n log n)
n_values_large = 1:20  # Para O(n^2) vs O(n^3), O(a^n) vs O(n!), y O(n!) vs O(n^n)

Resultados de la experimentación.

La simulación se llevó a cabo utilizando el lenguaje de programación Julia. Para la comparación de los órdenes de crecimiento, se definieron rangos de valores específicos. El rango de 1:100 se aplicó a aquellos órdenes que presentan un crecimiento más lento, mientras que los rangos más acotados de 1:20, 1:10 y 1:15 se utilizaron para evaluar órdenes con tasas de crecimiento potencialmente elevadas, como las funciones factoriales y exponenciales.

La definición de los rangos de comparación se implementó mediante el siguiente diccionario en Julia:

rangos_comparaciones = Dict(
    "O(1) vs O(log n)" => 1:100,
    "O(n) vs O(n log n)" => 1:100,
    "O(n²) vs O(n³)" => 1:20,
    "O(2ⁿ) vs O(n!)" => 1:15,
    "O(n!) vs O(nⁿ)" => 1:10
)

Para cada par de funciones se generó un gráfico comparativo.

Comparación: `O(1) vs O(log n)`

# Rangos adecuados para cada comparación
n_values = 1:100  # Para O(1) vs O(log n) y O(n) vs O(n log n)
n_values_large = 1:20  # Para O(n^2) vs O(n^3), O(a^n) vs O(n!), y O(n!) vs O(n^n)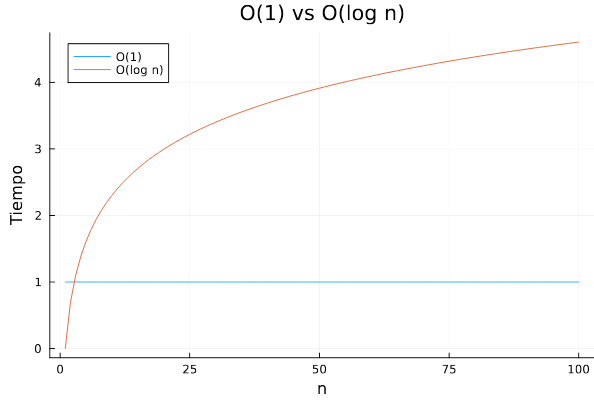

Gráfica 1: O(1) vs O(log n)

La Gráfica 1 obtenida resultado de comparar O(1) vs O(logn), se muestra la complejidad de los algoritmos, la línea azul muestra que el algoritmo O(1) es constante y que independientemente del tamaño de n sea igual a 10, 100 y 1000 el tiempo de ejecución siempre será el mismo. La línea naranja, representa O(logn), que es una curva creciente, pero es significativamente más lento que el crecimiento lineal, el grafico muestra la diferencia de rendimiento entre los algoritmos, los algoritmos de complejidad temporal son altamente eficientes ya que el tiempo necesario para completar la tarea es la misma incluso cuando cambia el tamaño de n, por otra parte, los algoritmos de complejidad temporal logarítmica se pueden considerar eficientes pero pueden volverse más lentos al cambiar la entrada de n por un valor mayor.

Comparación: `O(n) vs O(n log n)`

plot(n_values, [On.(n_values) Onlogn.(n_values)], label=["O(n)" "O(n log n)"], xlabel="n", ylabel="Tiempo", title="O(n) vs O(n log n)")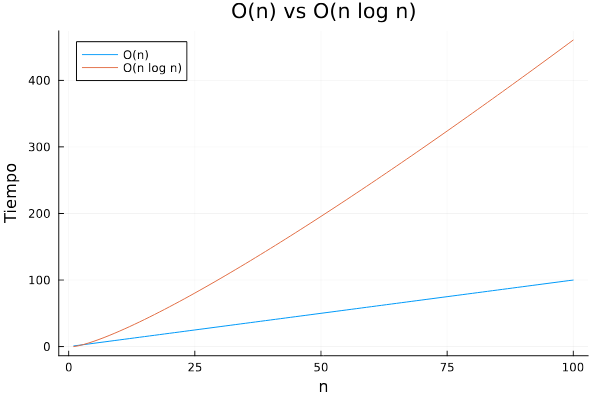

Gráfica 2: O(n) vs O(n log n)

El gráfico comparativo de los algoritmos O(n) vs O(n log n) en donde la línea azul es el algoritmo de tiempo lineal y la línea naranja es de tiempo lineal logarítmico. El algoritmo O(n log n) tiene un comportamiento más lento en comparación al algoritmo O(n), pero en medida que el tamaño de la entrada aumenta el tiempo de ejecución del algoritmo O(n log n) crecerá más rápido que O(n). Cuando la entrada n es grande. algoritmo O(n) es significativamente más rápido que el algoritmo O(n log n), esto resulta ser más perceptible en grandes cantidades de datos.

Comparación: `O(n^2) vs O(n^3)`

plot(n_values_large, [On2.(n_values_large) On3.(n_values_large)], label=["O(n^2)" "O(n^3)"], xlabel="n", ylabel="Tiempo", title="O(n^2) vs O(n^3)")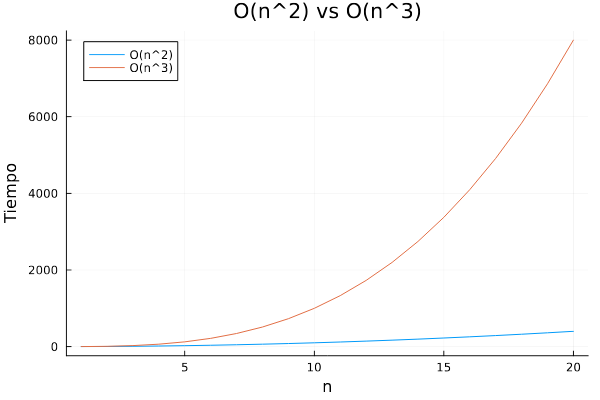

Gráfica 3: O(n^2) vs O(n^3)

La Gráfica 3, representa la complejidad temporal de dos algoritmos con diferentes órdenes de magnitud: O(n2) y O(n3). La línea azul representa el algoritmo con complejidad O(n2), mientras que la línea naranja representa el algoritmo con complejidad O(n3). Como se observa, la línea naranja crece más rápido que la línea azul, lo que indica que el algoritmo O(n3) tiene un tiempo de ejecución mucho mayor que el algoritmo O(n2) a medida que el tamaño de la entrada (n) aumenta. Este comportamiento se debe a que el algoritmo O(n3) realiza un número de operaciones proporcionales an3, mientras que el algoritmo O(n2) realiza un número de operaciones proporcionales an2. En otras palabras, si n = 10, el algoritmo O(n3) realizaría 1000 operaciones, mientras que el algoritmo O(n2) realizaría 100 operaciones. Esto ilustra por qué las funciones polinómicas de mayor grado, como O(n3), pueden llegar a ser extremadamente costosas para grandes entradas, mientras que las funciones de menor grado, como O(n^2), pueden manejar entradas más grandes con mayor eficiencia.

Comparación: `O(2n) vs O(n!)`

plot(n_values_large, [Oan.(n_values_large) Onfactorial.(n_values_large)], label=["O(2^n)" "O(n!)"], xlabel="n", ylabel="Tiempo", title="O(2^n) vs O(n!)")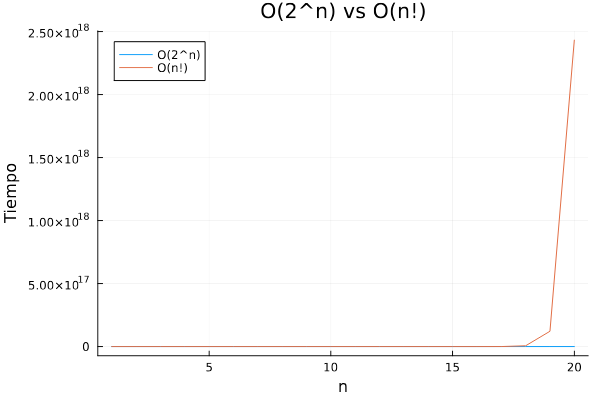

Gráfica 4: O(2^n) vs O(n!)

El gráfico resultante representa la comparación del tiempo de ejecución de dos algoritmos con diferentes complejidades: O(2n) y O(n!). La línea azul representa el algoritmo con complejidad O(2n), mientras que la línea naranja representa el algoritmo con complejidad O(n!). Se puede observar que el algoritmo O(2n) mantiene un tiempo de ejecución constante y relativamente bajo a medida que aumenta el valor de n. Por otro lado, el algoritmo O(n!) presenta un crecimiento exponencial del tiempo de ejecución a partir de un valor determinado de n, provocando un crecimiento abrupto. El tiempo de ejecución del algoritmo O(2n) crece a un ritmo mucho más lento que el algoritmo O(n!) lo que hace que éste último sea mucho más ineficiente para valores grandes de n.

Comparación: `O(2n) vs O(n!)`

Como n^n y n! crecen exponencialmente, se utilizó yscale = :log10 para facilitar su comparación visual:

plot(n_values_large,
     [BigInt.(factorial.(n_values_large)) [BigInt(n)^n for n in n_values_large]],
     label=["O(n!)" "O(n^n)"],
     xlabel="n", ylabel="Tiempo",
     title="O(n!) vs O(n^n)")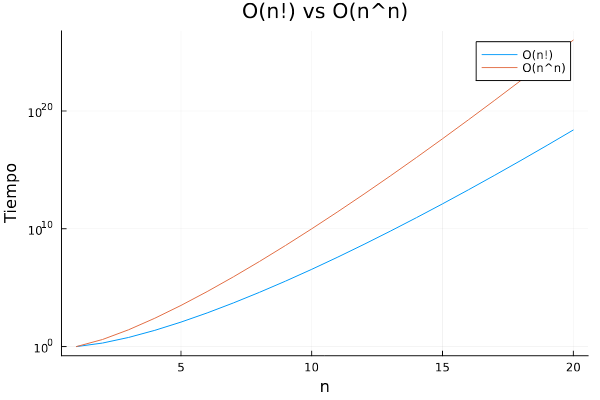

Gráfica 5: O(2n) vs O(n!)

De acuerdo con Knuth, D. 1973, el algoritmo factorial es una función que crece rápidamente, incluso más rápido que una función exponencial. En la Gráfica 5 se compara el crecimiento de dos funciones de complejidad algorítmica extremadamente alta: O(n!) (factorial de n) y O(n) (n elevado a la potencia de n). Esta comparación se realiza en el intervalo de valores de entrada n∈[1,20]. El eje horizontal (x) representa el tamaño de la entrada (n), mientras que el eje vertical (y) muestra el tiempo de ejecución simulado utilizando una escala logarítmica.

Ambas curvas exhiben un crecimiento exponencial extremo, una característica distintiva de las complejidades no polinómicas. Este crecimiento, aunque inicialmente lento para valores muy pequeños de n, se dispara de manera abrupta a partir de valores moderados, situados alrededor de n=6 a 8. Este comportamiento subraya la rapidez con la que los tiempos de ejecución pueden volverse prohibitivos para algoritmos con estas complejidades a medida que el tamaño de la entrada aumenta ligeramente.

Para ilustrar la magnitud de estos crecimientos, consideremos un valor de entrada de n≈15. En este punto, el tiempo de ejecución simulado para un algoritmo con complejidad O(n!) ya supera las 1011 unidades. En contraste, un algoritmo con complejidad O(nn) alcanza valores del orden de 1020 incluso antes de que n llegue a 20. Estas cifras astronómicas resaltan la impracticabilidad de estos algoritmos para incluso tamaños de entrada relativamente pequeños.

Tiempos de ejecución

El siguiente bloque de código evalúa y compara el comportamiento de distintas funciones de complejidad algorítmica para varios tamaños de entrada n:

n_sizes = [100, 1000, 10000, 100000]

df = DataFrame(n = Int[], O1 = Float64[], Ologn = Float64[], On = Float64[],
               Onlogn = Float64[], On2 = Float64[], On3 = Float64[],
               Oan = Float64[], Onfactorial = Float64[], Onn = Float64[])

for n in n_sizes
    n_big = big(n)
    push!(df, (n, O1(n), Ologn(n), On(n), Onlogn(n), On2(n), On3(n),
               Oan(n), Onfactorial(n_big), Onn(n_big)))
end

println(df)

4×10 DataFrame
 Row │ n       O1       Ologn     On        Onlogn         On2         On3      Oan      Onfactorial    Onn       
     │ Int64   Float64  Float64   Float64   Float64        Float64     Float64  Float64  Float64        Float64   
─────┼────────────────────────────────────────────────────────────────────────────────────────────────────────────
   1 │    100      1.0   4.60517     100.0    460.517      10000.0      1.0e6       0.0    9.33262e157    1.0e200
   2 │   1000      1.0   6.90776    1000.0   6907.76           1.0e6    1.0e9       0.0  Inf            Inf
   3 │  10000      1.0   9.21034   10000.0  92103.4            1.0e8    1.0e12      0.0  Inf            Inf
   4 │ 100000      1.0  11.5129   100000.0      1.15129e6      1.0e10   1.0e15      0.0  Inf            Inf

Tabla 1. Tiempos de ejecución

La Tabla 1 compara los tiempos de ejecución simulados (en nanosegundos) de algoritmos con distintas órdenes de complejidad: O(1), O(logn), O(n), O(nlogn), O(n2), O(n3), O(2n), O(n!) y O(nn), considerando tamaños de entrada de n=100,1000,10000 y 100000. Estos valores ilustran cómo escala el tiempo requerido a medida que aumenta el tamaño de los datos.

Como se esperaba, la complejidad O(1) se mantiene constante en 1 nanosegundo para cualquier tamaño de entrada. Este comportamiento confirma que los algoritmos de tiempo constante no dependen de la magnitud del problema, ejecutando una única operación independientemente de la cantidad de datos.

La complejidad O(logn) exhibe un crecimiento muy lento y progresivo. Aunque aumenta con n, su incremento es mínimo incluso en escalas grandes, lo que la convierte en una complejidad altamente eficiente. Por ejemplo, para n=100000, el tiempo apenas se diferencia del registrado para n=100.

Los algoritmos con complejidad O(n) escalan de forma lineal: el tiempo de ejecución se incrementa en proporción directa al tamaño de la entrada. Esto se evidencia al observar que para n=100000, el tiempo simulado es de aproximadamente 100000 ns, lo que demuestra un comportamiento predecible y manejable incluso con grandes volúmenes de datos.

En contraste, las complejidades O(n2) y O(n3) muestran un crecimiento polinómico mucho más pronunciado. Por ejemplo, para n=100, se obtienen tiempos de 10000 ns y 1000000 ns respectivamente, lo cual anticipa una escalabilidad deficiente. Tal como señalan Cormen et al. (2009), los algoritmos con complejidades polinómicas elevadas resultan prácticos solo para tamaños de entrada pequeños, ya que rápidamente se vuelven inviables en escenarios reales con grandes conjuntos de datos.

Finalmente, las clases de complejidad exponencial (como O(2n)) y superexponencial o hiperexponencial (como O(n!) y O(nn)) representan órdenes de crecimiento que exceden ampliamente los límites computacionales prácticos. Estas funciones crecen tan rápidamente que, incluso para valores moderados de n, los tiempos de ejecución simulados se vuelven extremadamente altos o directamente incalculables (por ejemplo, ∞ para O(nn)). Como indica Bhargava (2016), los algoritmos con este tipo de complejidades se vuelven inoperantes ante tamaños de entrada sorprendentemente pequeños, y su aplicabilidad se restringe a contextos altamente especializados o académicos.

Referencias

Bhargava, A. (2016). Grokking algorithms: Video edition. Manning Publications. 256 pág.
Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2009). Introducción a los algoritmos (4ª ed.). MIT Press & McGraw- Hill. ISBN 9780262533058.1312 págs.
Knuth, D. (1973). The Art of Computer Programming: Volume 3: Sorting and Searching. Consultado el 04 de febrero de 2025. Disponible en https://openlibrary.org/books/OL657041M/The_art_of_computer_programming

Maestría en Ciencia de datos e información.

Introducción

Definición de funciones de complejidad en Julia

Resultados de la experimentación.

Comparación: O(1) vs O(log n)

Comparación: O(n) vs O(n log n)

Comparación: O(n^2) vs O(n^3)

Comparación: O(2n) vs O(n!)

Comparación: O(2n) vs O(n!)

Tiempos de ejecución

Referencias

Comparación: `O(1) vs O(log n)`

Comparación: `O(n) vs O(n log n)`

Comparación: `O(n^2) vs O(n^3)`

Comparación: `O(2n) vs O(n!)`

Comparación: `O(2n) vs O(n!)`