Experimentos y análisis de algoritmos de intersección de conjuntos
Introducción.
El problema de la intersección de listas ordenadas es fundamental en diversas aplicaciones informáticas como motores de búsqueda, sistemas de recuperación de información y bases de datos.
Los algoritmos de intersección se emplean para identificar los elementos comunes presentes en múltiples listas ordenadas, una operación esencial en diversas aplicaciones, incluyendo motores de búsqueda, sistemas de bases de datos relacionales y no relacionales, y el procesamiento de consultas en bases de datos de grafos (Zobel & Moffat, 2006).
Debido a la variedad de contextos en los que se aplica, existen distintos algoritmos que resuelven esta tarea de formas más o menos eficientes, dependiendo del tamaño de las listas y su distribución.
Este reporte se enfoca en comparar el rendimiento de cinco algoritmos representativos: Melding, Baez-Yates con búsqueda binaria (BY-Binary), Baez-Yates con búsqueda no acotada B1 (BY-B1), Baez-Yates con búsqueda no acotada B2 (BY-B2), y Barbay-Kenyon (BK).
El objetivo principal de este trabajo es comparar el rendimiento de estos algoritmos en diferentes escenarios, variando el número de listas a intersectar. Se busca proporcionar una evaluación empírica de la eficiencia de estos algoritmos, destacando sus características y limitaciones.
Implementación de código.
Para comenzar con la implementación el código se divide en diferentes secciones, primero se utilizaron varias librerías las cuales cumplen funciones específicas:
gzip: Permite la lectura de archivos comprimidos con el formato
.gz. Es utilizada para descomprimir los archivos JSON que contienen las listas de datos, permitiendo así una lectura eficiente y directa desde archivos comprimidos. (Python documents, 2025).json: Se encarga de la carga y manipulación de datos en formato JSON.
time: Proporciona funciones para medir el tiempo de ejecución de los algoritmos.
random: Se utilizó para seleccionar subconjuntos aleatorios de listas del conjunto de datos original, permitiendo realizar múltiples experimentos con combinaciones diferentes y asegurar un análisis más amplio.
heapq: Implementa una estructura de datos de heap (montículo) basada en listas, y es clave en la implementación del algoritmo Barbay-Kenyon (BK).
matplotlib.pyplot y seaborn: Estas librerías se utilizarón para la visualización de los resultados mediante la generación de boxplots.
statistics: Provee funciones para el cálculo de medidas descriptivas como la media y la mediana.
A continuación se muestra el bloque de código con las librerías implementadas:
import gzip
import json
import time
import statistics
import matplotlib.pyplot as plt
import numpy as npPosterior a la carga de la librerías se hizo la carga de datos lo que permitió trabajar con los archivos comprimidos en formato Json (.Json.gz) esto facilitó una correcta descompresión de los archivos a utilizar.
# Función para leer archivos JSON comprimidos
def leer_json_gz(ruta_archivo):
try:
with gzip.open(ruta_archivo, 'rt') as f:
data = json.load(f)
print(f"Archivo leído exitosamente: {ruta_archivo}")
return data
except FileNotFoundError:
print(f"Error: El archivo no se encontró en la ruta: {ruta_archivo}")
return None
except gzip.BadGzipFile:
print(f"Error: El archivo no parece ser un archivo gzip válido: {ruta_archivo}")
return None
except json.JSONDecodeError:
print(f"Error: El archivo no contiene JSON válido: {ruta_archivo}")
return None
except Exception as e:
print(f"Ocurrió un error al leer el archivo {ruta_archivo}: {e}")
return None
# Función para cargar datos de los archivos
def cargar_datos(ruta_base, nombres_archivos):
datos_todos_conjuntos = {}
for nombre_conjunto, nombre_archivo in nombres_archivos.items():
ruta_completa = f"{ruta_base}/{nombre_archivo}"
print(f"Leyendo archivo para {nombre_conjunto}: {ruta_completa}")
datos_todos_conjuntos[nombre_conjunto] = leer_json_gz(ruta_completa)
return datos_todos_conjuntosAlgoritmos de intersección.
Búsqueda binaria.
La búsqueda binaria es un algoritmo eficiente para encontrar un elemento específico dentro de un conjunto de datos ordenado. La idea principal de la búsqueda binaria es dividir repetidamente la porción de la lista que podría contener el elemento, hasta reducir las posibles ubicaciones a solo una. Devuelve la posición del elemento objetivo y el número de comparaciones realizadas. La búsqueda binaria tiene una complejidad temporal de O(log n) (Cormen et al., 2022).
# Función de búsqueda binaria
def binarysearch(arr, target, start, stop):
low, high = start, stop
comparaciones = 0
while low <= high:
mid = (low + high) // 2
comparaciones += 1
if 0 <= mid < len(arr):
if arr[mid] == target:
return mid, comparaciones
elif arr[mid] < target:
low = mid + 1
else:
high = mid - 1
else:
if mid < 0:
low = 0
else:
high = len(arr) - 1
continue
return high + 1, comparacionesAlgoritmo de Baeza-Yates.
baezayates_recursive(output, A, a_sp, a_ep, B, b_sp, b_ep, findpos) y baezayates(A, B, findpos=binarysearch): Implementan el algoritmo de Baeza-Yates, un algoritmo de divide y vencerás para la intersección de dos listas ordenadas.
Este algoritmo es especialmente eficiente cuando una de las listas es significativamente más corta que la otra (Baeza-Yates & Perleberg, 1992). La idea principal es seleccionar un elemento mediano de la lista más corta y buscarlo en la lista más larga. Basado en el resultado de la búsqueda, el problema se divide en subproblemas más pequeños.
El algoritmo de Baeza-Yates tiene una complejidad temporal de O(n log m), donde n es la longitud de la lista más corta y m es la longitud de la lista más larga.
# Algoritmo de Baez y Yates
def baezayates_recursive(output, A, a_sp, a_ep, B, b_sp, b_ep, findpos):
if a_ep < a_sp or b_ep < b_sp:
return output, 0
median = A[(a_sp + a_ep) // 2]
medpos, comps = findpos(B, median, b_sp, b_ep)
matches = (medpos < len(B) and median == B[medpos])
comparaciones = comps
output_left, comps_left = baezayates_recursive(output, A, a_sp, (a_sp + a_ep) // 2 - 1, B, b_sp, medpos - (1 if matches else 0), findpos)
comparaciones += comps_left
if matches:
output.append(median)
output_right, comps_right = baezayates_recursive(output, A, (a_sp + a_ep) // 2 + 1, a_ep, B, medpos + (1 if matches else 0), b_ep, findpos)
comparaciones += comps_right
return output, comparaciones
def baezayates(A, B, findpos=binarysearch):
output = []
output_final, comparaciones = baezayates_recursive(output, sorted(A), 0, len(A) - 1, sorted(B), 0, len(B) - 1, findpos)
return output_final, comparacionesBúsqueda no acotada.
Se implementaron dos variantes de búsqueda no acotada unbounded_search_b1(arr, target, start, stop) y unbounded_search_b2(arr, target, start, stop). Estas búsquedas son útiles cuando no se conoce el límite superior del rango donde se encuentra el elemento objetivo, lo cual puede ocurrir en ciertas aplicaciones.
La búsqueda no acotada B1 realiza una expansión lineal, mientras que B2 realiza una expansión exponencial. Lo anterior se muestra en el bloque de código siguiente:
# Búsqueda No Acotada B1 (Búsqueda con Expansión Lineal)
def unbounded_search_b1(arr, target, start, stop):
comparaciones = 0
if not arr:
return -1, comparaciones
k = 1
while True:
index = start + k - 1
comparaciones += 1
if index < len(arr) and arr[index] >= target:
low, high = start, index
while low <= high:
mid = (low + high) // 2
comparaciones += 1
if 0 <= mid < len(arr):
if arr[mid] == target:
return mid, comparaciones
elif arr[mid] < target:
low = mid + 1
else:
high = mid - 1
else:
break
return high + 1, comparaciones
elif index >= len(arr):
return len(arr), comparaciones
k *= 2
# Búsqueda No Acotada B2 (Búsqueda con Expansión Exponencial)
def unbounded_search_b2(arr, target, start, stop):
comparaciones = 0
if not arr:
return -1, comparaciones
k = 1
index = start
while index < len(arr) and arr[index] < target:
index = start + k
comparaciones += 1
k *= 2
low = start + (k // 4) if k > 1 else start
high = min(start + k, len(arr) - 1)
while low <= high:
mid = (low + high) // 2
comparaciones += 1
if 0 <= mid < len(arr):
if arr[mid] == target:
return mid, comparaciones
elif arr[mid] < target:
low = mid + 1
else:
high = mid - 1
else:
break
return high + 1, comparacionesAlgoritmo Baeza-Yates.
barbay_kenyon(lists): Implementa el algoritmo de Barbay & Kenyon, el cual utiliza una cola de prioridad (heap) para intersectar múltiples listas ordenadas de manera eficiente. Este algoritmo mantiene un heap de los elementos más pequeños de cada lista y extrae repetidamente el mínimo, verificando si está presente en todas las listas. (Baeza-Yates y Perleberg, 1998), Es particularmente eficiente cuando se intersectan muchas listas.
def baezayates_b1(A, B):
return baezayates(A, B, findpos=unbounded_search_b1)
def baezayates_b2(A, B):
return baezayates(A, B, findpos=unbounded_search_b2)Algoritmo de Barbay y Kenyon.
El algoritmo de Barbay & Kenyon (Barbay & Kenyon, 2002), utiliza una cola de prioridad (heap) para intersectar múltiples listas ordenadas de manera eficiente.
Este algoritmo mantiene un heap de los elementos más pequeños de cada lista y extrae repetidamente el mínimo, verificando si está presente en todas las listas. Es particularmente eficiente cuando se intersectan muchas listas.
def barbay_kenyon(lists):
comparaciones = 0
resultados = []
listas_ordenadas = [sorted(lista) for lista in lists]
n = len(listas_ordenadas)
# Inicializar un heap.
heap = [(lista[0], i, 0) for i, lista in enumerate(listas_ordenadas) if lista]
import heapq
heapq.heapify(heap)
while heap:
val_min, lista_min_index, indice_min = heapq.heappop(heap)
presente_en_todas = True
for i in range(n):
if i != lista_min_index:
pos, comps = binarysearch(listas_ordenadas[i], val_min, 0, len(listas_ordenadas[i]) - 1)
comparaciones += comps
if pos >= len(listas_ordenadas[i]) or listas_ordenadas[i][pos] != val_min:
presente_en_todas = False
break
if presente_en_todas:
resultados.append(val_min)
if indice_min + 1 < len(listas_ordenadas[lista_min_index]):
nuevo_indice = indice_min + 1
heapq.heappush(heap, (listas_ordenadas[lista_min_index][nuevo_indice], lista_min_index, nuevo_indice))
return resultados, comparacionesAlgoritmo de Melding.
El algoritmo de Melding compara los elementos en la cabeza de cada lista ordenada. Si todos los elementos actuales son iguales, este valor se agrega al resultado de la intersección. Si no, se descartan los menores y se continúa con los elementos restantes. Este enfoque se basa en la sincronización progresiva de las listas hasta encontrar coincidencias. Su simplicidad lo hace accesible para listas de tamaños similares (Knuth, 1998).
# Algoritmo de Melding
def melding(lists):
if not lists:
return [], 0
indices = [0] * len(lists)
intersection = []
comparaciones = 0
while True:
current_element = lists[0][indices[0]]
all_equal = True
for i in range(1, len(lists)):
while indices[i] < len(lists[i]) and lists[i][indices[i]] < current_element:
indices[i] += 1
comparaciones += 1
comparaciones += 1
if indices[i] >= len(lists[i]) or lists[i][indices[i]] != current_element:
all_equal = False
break
if all_equal:
intersection.append(current_element)
indices = [index + 1 for index in indices]
else:
min_val = float('inf')
list_to_advance = -1
for i in range(len(lists)):
if indices[i] < len(lists[i]):
comparaciones += 1
if lists[i][indices[i]] < min_val:
min_val = lists[i][indices[i]]
list_to_advance = i
if list_to_advance == -1:
break
indices[list_to_advance] += 1
if any(indices[i] >= len(lists[i]) for i in range(len(lists))):
break
return intersection, comparacionesFunciones de experimentación.
Para ejecutar los experimentos para cada conjunto de datos y por cada algoritmo se utilizo una función que permite ejecutar las pruebas, la cual es ejecutar_experimentos(datos_todos_conjuntos, algorithms, num_repetitions=50) en donde se establece que se realicen 50 repeticiones para minimizar algo sesgo que pudieran tener los resultados.
Para poder observar el comportamiento de los datos se generaron gráficos utilizando boxplot, se elaboraron gráficos para el tiempo de ejecución, el número de comparaciones y la longitud de las intersecciones, esto re realizo con ayuda de la función: def crear_boxplot(resultados, nombre_conjunto, tipo_metrica, ylabel, filename):
Finalmente en la parte final del código se define la ruta de los archivos de datos, los nombres de los archivos y los algoritmos a ejecutar. Luego, se cargan los datos, se ejecutan los experimentos y se generan los gráficos boxplot.
La implementación del código se muestra en el código siguiente:
def ejecutar_experimentos(datos_todos_conjuntos, algorithms, num_repetitions=50):
resultados = {}
for nombre_conjunto, datos_conjunto in datos_todos_conjuntos.items():
resultados[nombre_conjunto] = {}
print(f"\nEjecutando experimentos para {nombre_conjunto}:")
for alg_name, alg in algorithms.items():
tiempos = []
comparaciones_totales = []
longitudes_intersecciones = []
print(f" Ejecutando algoritmo {alg_name}:")
for listas in datos_conjunto:
if nombre_conjunto == "Conjunto A":
if len(listas) != 2:
print(f"Advertencia: Se esperaba un par de listas para {nombre_conjunto}, se encontró {len(listas)}. Saltando.")
continue
listas_alg = listas
elif nombre_conjunto == "Conjunto B":
if len(listas) != 3:
print(f"Advertencia: Se esperaba una tripleta de listas para {nombre_conjunto}, se encontró {len(listas)}. Saltando.")
continue
listas_alg = listas
elif nombre_conjunto == "Conjunto C":
if len(listas) != 4:
print(f"Advertencia: Se esperaba una tetrapleta de listas para {nombre_conjunto}, se encontró {len(listas)}. Saltando.")
continue
listas_alg = listas
else:
print(f"Advertencia: Conjunto desconocido: {nombre_conjunto}. Saltando.")
continue
tiempos_repeticiones = []
comparaciones_repeticiones = []
longitudes_repeticiones = []
for _ in range(num_repetitions):
start_time = time.time()
if alg_name == "Melding":
interseccion, comparaciones = alg(listas_alg)
elif alg_name.startswith("BY"):
if len(listas_alg) < 2:
print(f"Error: Se necesitan al menos dos listas para BY en {nombre_conjunto}. Saltando.")
comparaciones = 0
interseccion = []
else:
list1 = listas_alg[0]
list2 = listas_alg[1]
interseccion, comparaciones = alg(list1, list2)
elif alg_name == "BK":
interseccion, comparaciones = alg(listas_alg)
else:
print(f"Algoritmo desconocido: {alg_name}. Saltando.")
comparaciones = 0
interseccion = []
end_time = time.time()
tiempos_repeticiones.append(end_time - start_time)
comparaciones_repeticiones.append(comparaciones)
longitudes_repeticiones.append(len(interseccion))
tiempos.extend(tiempos_repeticiones)
comparaciones_totales.extend(comparaciones_repeticiones)
longitudes_intersecciones.extend(longitudes_repeticiones)
resultados[nombre_conjunto][alg_name] = {
"tiempos": tiempos,
"comparaciones": comparaciones_totales,
"longitudes": longitudes_intersecciones
}
return resultados
def crear_boxplot(resultados, nombre_conjunto, tipo_metrica, ylabel, filename):
datos_boxplot = []
etiquetas = []
for alg_name, result in resultados[nombre_conjunto].items():
datos_boxplot.append(result[tipo_metrica])
etiquetas.append(alg_name)
plt.figure(figsize=(10, 6))
plt.boxplot(datos_boxplot, labels=etiquetas)
plt.title(f"Boxplot de {ylabel} para {nombre_conjunto}")
plt.xlabel("Algoritmo")
plt.ylabel(ylabel)
plt.grid(True)
plt.savefig(filename)
plt.close()
# Ruta de datos
ruta_base = "/home/Catana/Documents/analisis de algoritmos/archivos"
nombres_archivos = {
"Conjunto A": "postinglists-for-intersection-A-k=2.json.gz",
"Conjunto B": "postinglists-for-intersection-B-k=3.json.gz",
"Conjunto C": "postinglists-for-intersection-C-k=4.json.gz"
}
# Definir los algoritmos a ejecutar
algorithms = {
"Melding": melding,
"BY-Binary": baezayates,
"BY-B1": baezayates_b1,
"BY-B2": baezayates_b2,
"BK": barbay_kenyon,
}
# Cargar los datos
datos_todos_conjuntos = cargar_datos(ruta_base, nombres_archivos)
if datos_todos_conjuntos:
# Verificar si algún conjunto de datos no se cargó correctamente
if any(datos_todos_conjuntos[nombre] is None for nombre in datos_todos_conjuntos):
print("Error: No se pudieron cargar todos los conjuntos de datos correctamente. Revise los mensajes de error durante la carga.")
else:
# Ejecutar los experimentos solo si todos los datos se cargaron
resultados_experimentos = ejecutar_experimentos(datos_todos_conjuntos, algorithms, num_repetitions=10)
for nombre_conjunto in resultados_experimentos:
crear_boxplot(resultados_experimentos, nombre_conjunto, "tiempos", "Tiempo (segundos)", f"tiempo_{nombre_conjunto}.png")
crear_boxplot(resultados_experimentos, nombre_conjunto, "comparaciones", "Número de Comparaciones", f"comparaciones_{nombre_conjunto}.png")
crear_boxplot(resultados_experimentos, nombre_conjunto, "longitudes", "Longitud de la Intersección", f"longitud_{nombre_conjunto}.png")
print("\nGráficos boxplot generados y guardados.")
print("\nAnálisis de los resultados:")
for nombre_conjunto, resultados_conjunto in resultados_experimentos.items():
print(f"\nResultados para {nombre_conjunto}:")
for alg_name, resultados_alg in resultados_conjunto.items():
tiempos = resultados_alg["tiempos"]
comparaciones = resultados_alg["comparaciones"]
longitudes = resultados_alg["longitudes"]
tiempo_medio = statistics.mean(tiempos)
tiempo_mediana = statistics.median(tiempos)
comparaciones_media = statistics.mean(comparaciones)
comparaciones_mediana = statistics.median(comparaciones)
longitud_media = statistics.mean(longitudes)
longitud_mediana = statistics.median(longitudes)
print(f"\n Algoritmo: {alg_name}")
print(f" Tiempo de ejecución:")
print(f" Media: {tiempo_medio:.6f} segundos")
print(f" Mediana: {tiempo_mediana:.6f} segundos")
print(f" Número de comparaciones:")
print(f" Media: {comparaciones_media:.2f}")
print(f" Mediana: {comparaciones_mediana:.2f}")
print(f" Longitud de la intersección:")
print(f" Media:{longitud_media:.2f}")
print(f" Mediana:{longitud_mediana:.2f}")
print(f"\n Análisis comparativo para {nombre_conjunto}:")
tiempos_algoritmos = {alg_name: resultados_alg["tiempos"] for alg_name, resultados_alg in resultados_conjunto.items()}
comparaciones_algoritmos = {alg_name: resultados_alg["comparaciones"] for alg_name, resultados_alg in resultados_conjunto.items()}
longitudes_algoritmos = {alg_name: resultados_alg["longitudes"] for alg_name, resultados_alg in resultados_conjunto.items()}
algoritmo_mas_rapido = min(tiempos_algoritmos, key=lambda k: statistics.mean(tiempos_algoritmos[k]))
algoritmo_mas_lento = max(tiempos_algoritmos, key=lambda k: statistics.mean(tiempos_algoritmos[k]))
print(f" El algoritmo más rápido es: {algoritmo_mas_rapido}")
print(f" El algoritmo más lento es: {algoritmo_mas_lento}")
longitud_maxima = max(longitudes_algoritmos, key=lambda k: statistics.mean(longitudes_algoritmos[k]))
longitud_minima = min(longitudes_algoritmos, key=lambda k: statistics.mean(longitudes_algoritmos[k]))
print(f" El algoritmo con la interseccion mas larga es: {longitud_maxima}")
print(f" El algoritmo con la interseccion mas corta es: {longitud_minima}")
else:
print("Error: No se cargaron datos. No se pueden ejecutar los experimentos.")Resultados.
Los experimentos se realizaron utilizando tres conjuntos de datos (Conjunto A, Conjunto B y Conjunto C), Se comparó el rendimiento de los algoritmos de Melding, Baeza-Yates (con búsqueda binaria, B1 y B2) y Barbay & Kenyon en términos de tiempo de ejecución y número de comparaciones.
Los resultados muestran que el rendimiento de los algoritmos varía significativamente dependiendo del conjunto de datos y la métrica considerada. En general, el algoritmo de Melding tiende a ser más rápido para conjuntos de datos con listas más cortas, mientras que el algoritmo de Baeza-Yates, especialmente con búsqueda binaria, muestra un mejor rendimiento para conjuntos de datos con listas más largas.
El algoritmo de Barbay & Kenyon, diseñado para múltiples listas, se desempeña de manera competitiva, especialmente en los conjuntos B y C. Estas observaciones sugieren que la elección del algoritmo más adecuado depende en gran medida de las características específicas de los datos de entrada, consultar Grafica 1 a Gráfica 3.
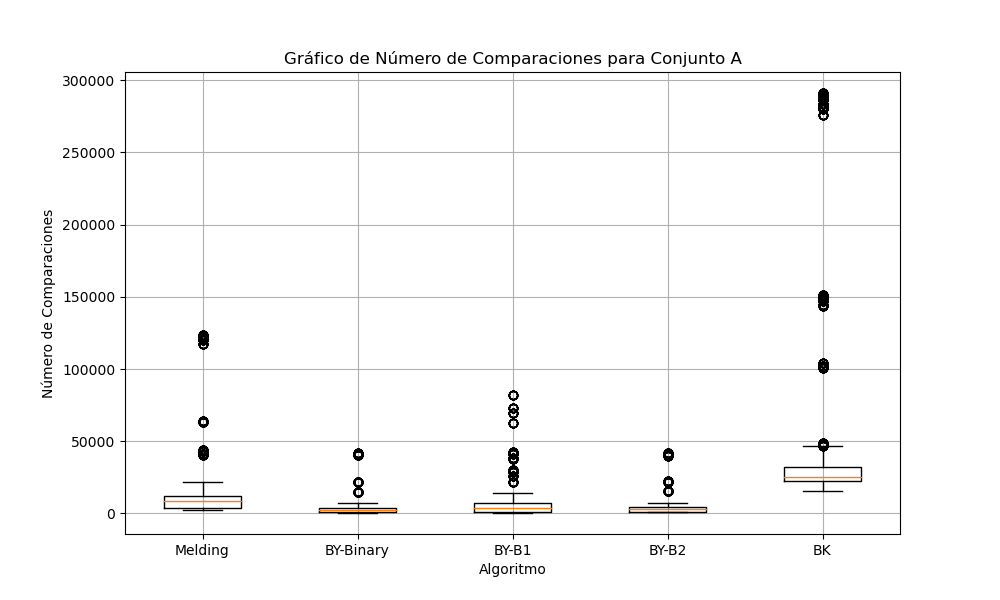
Gráfica 1: Comparaciones para conjunto A
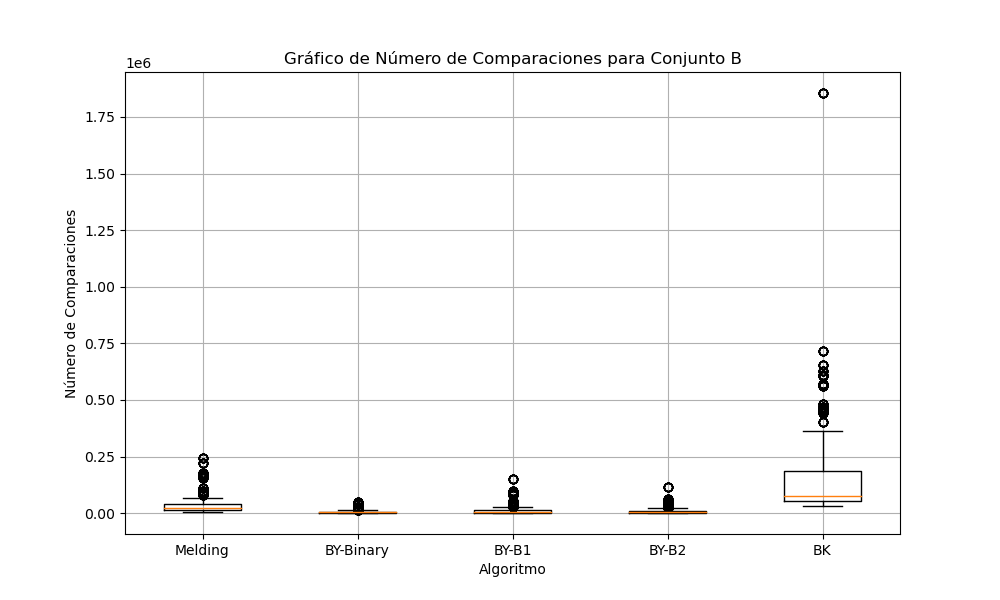
Gráfica 2: Comparaciones para conjunto B
Melding comienza a incrementar su número de comparaciones. Los algoritmos BY muestran un comportamiento estable, con BY-Binary realizando la menor cantidad de comparaciones. BK se distancia aún más, realizando muchas más comparaciones que los demás.
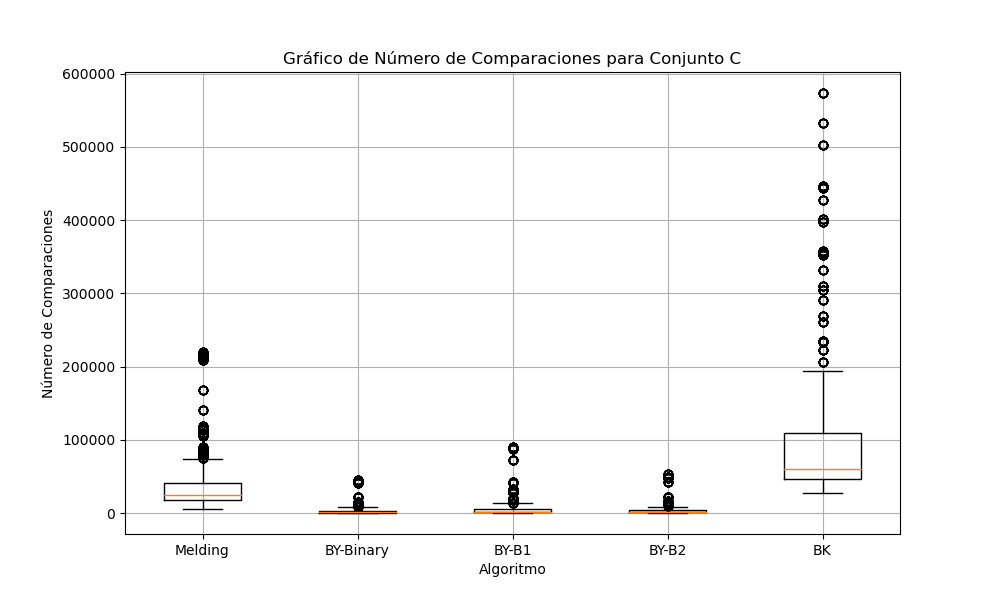
Gráfica 3: Comparaciones para conjunto C
Para el casdo del conjunto C, elalgoritmo de Melding aumenta considerablemente el número de comparaciones. Los algoritmos BY son los más eficientes en términos de comparaciones, y BK es el que más comparaciones realiza. Este comportamiento se alinea con lo que se observa en los gráficos de tiempo de ejecución.
Ahora bien los gráficos de longitud de las intersecciones (Gráfica 4 a 6) muestran que todos los algoritmos producen intersecciones de longitudes similares para un mismo conjunto de datos, lo que indica que las implementaciones funcionan correctamente.
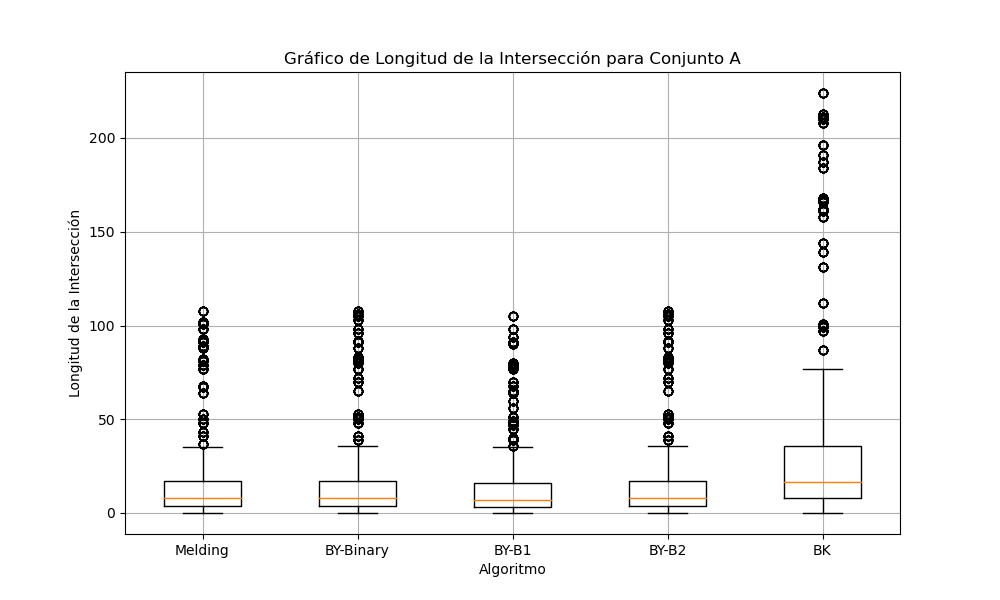
Gráfica 4: Longitud de intersecciones para conjunto A
en el conjunto A se muestra que la longitud de las intersecciones es bastante similar entre los algoritmos, aunque BK presenta un poco más de variabilidad.
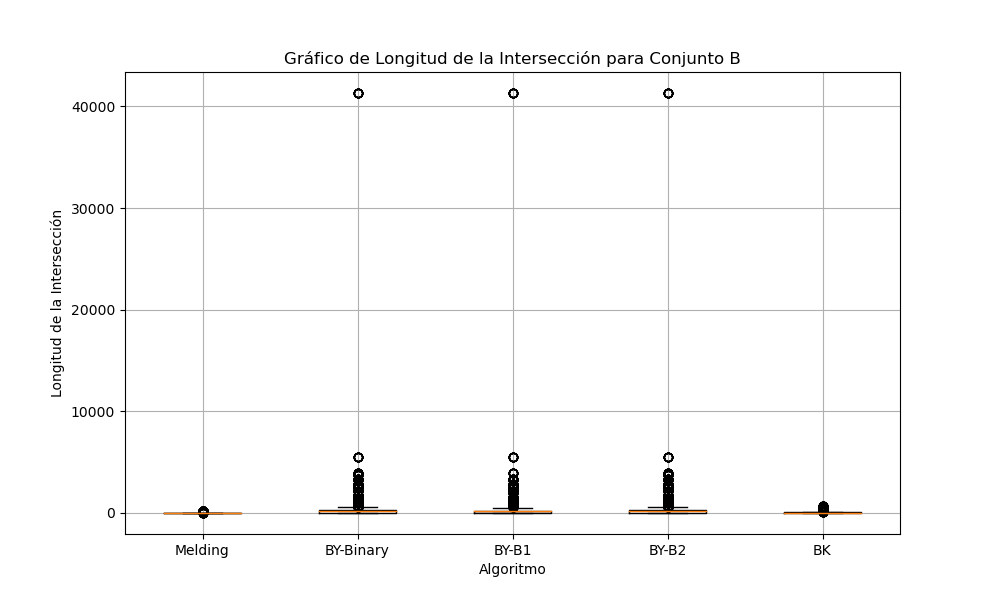
Gráfica 5: Longitud de intersecciones para conjunto B
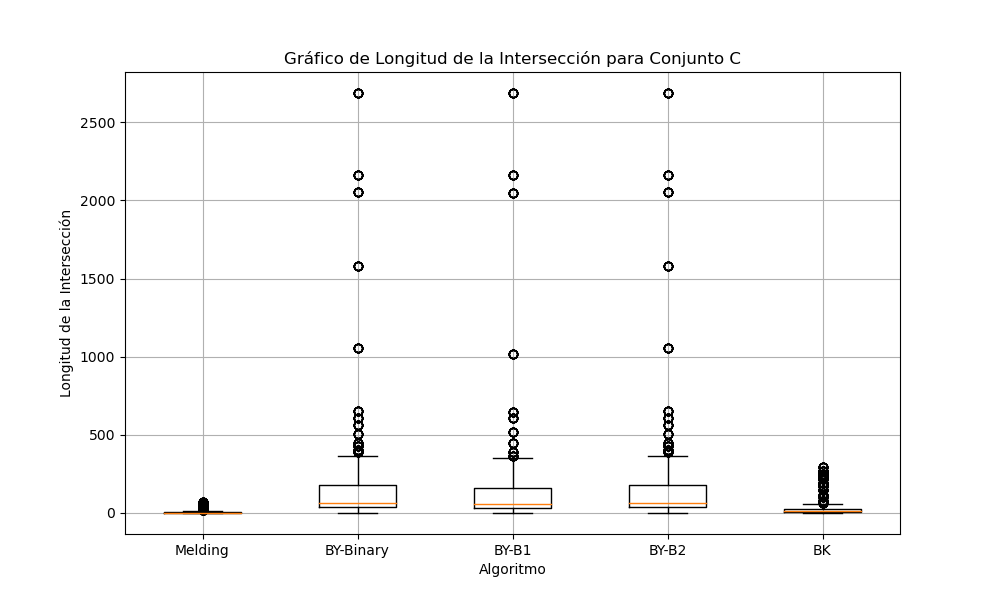
Gráfica 6: Longitud de intersecciones para conjunto C.
Para los conjuntos B y C, se observa que los algoritmos están generando intersecciones de longitudes similares. Esto es importante, ya que sugiere que todos los algoritmos están encontrando los elementos comunes correctamente.
Con respecto a los tiempos de ejecución para el conjunto A, el gráfico de tiempos de ejecución deja ver que el algoritmo de Melding, es bueno en velocidad y por su parte los algortimos de Baeza-Yates (BY-Binary, BY-B1, BY-B2) son competitivos, con BY-Binary mostrando una ligera ventaja y menor variabilidad. BK es el más lento y variable en este conjunto, consultar Gráfica 7.
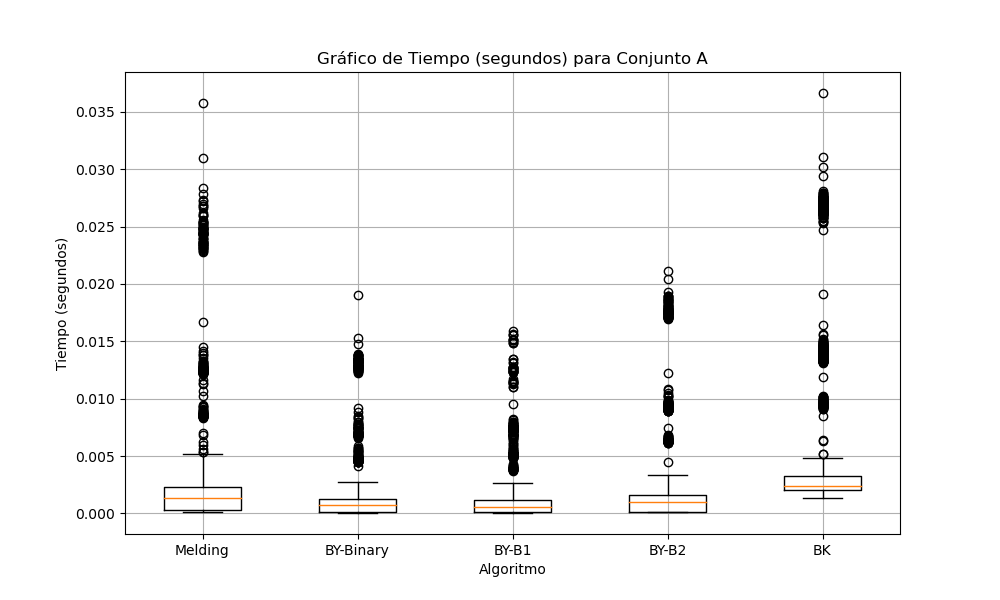
Gráfica 7: Tiempo en segundos para conjunto A.
En el conjunto B (Gráfica 8), el algoritmo de Melding comienza a mostrar un incremento en el tiempo de ejecución y mayor variabilidad. BY-Binary sigue siendo el algoritmo más eficiente y BK se muestra con el más lento y con la mayor dispersión en los tiempos.
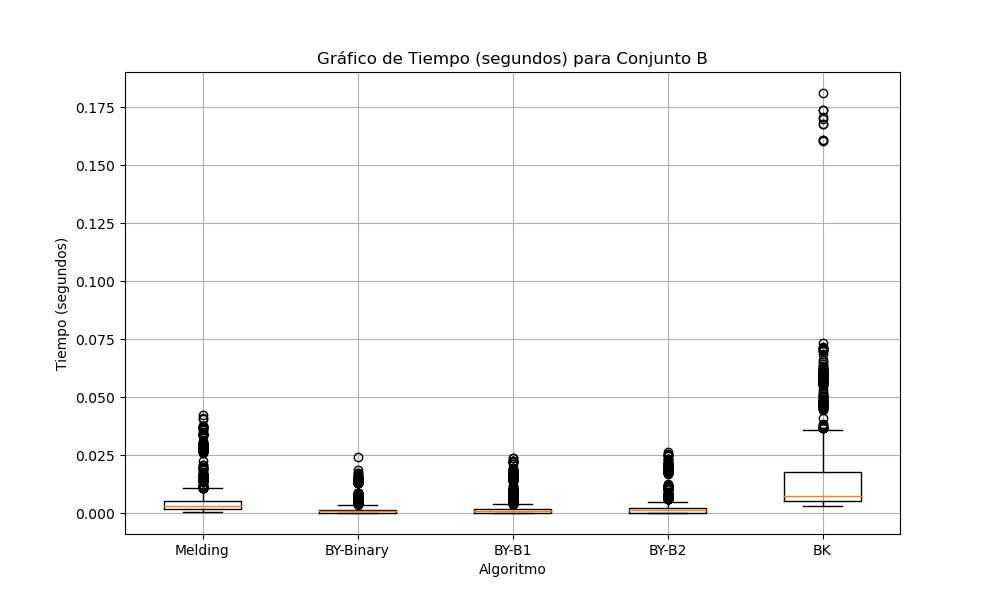
Gráfica 8: Tiempo en segundos para conjunto B.
Finalmente en el conjunto C (Gráfico 9), en comparación conla tendencia observada en el Conjunto B. Melding es significativamente más lento y variable. BY-Binary mantiene su eficiencia. BK es el algoritmo con el peor desempeño en tiempo de ejecución.
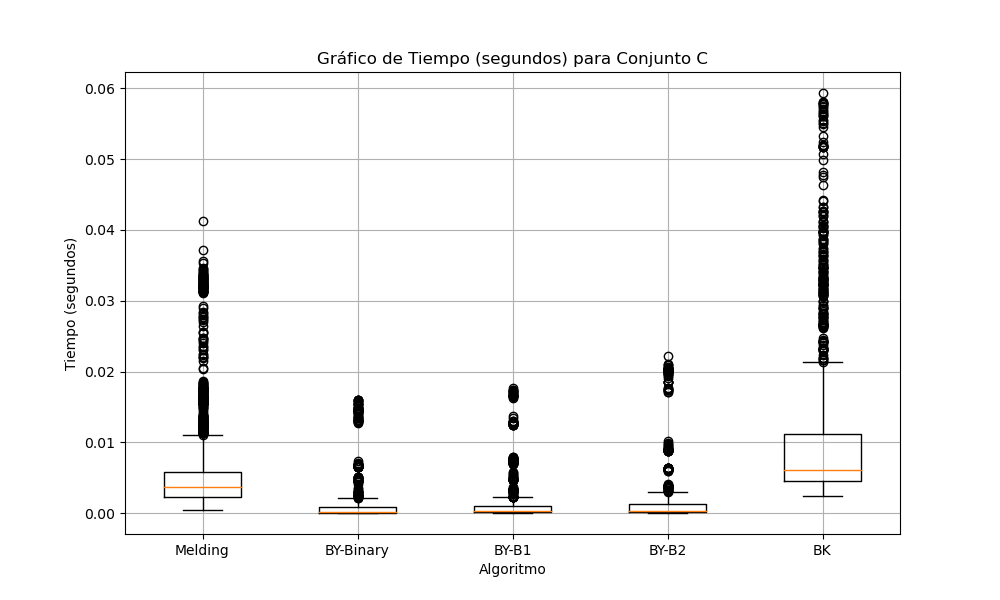
Gráfica 9: Tiempo en segundos para conjunto C.
Conclusiones.
A partir de los resultados presentados, se pueden concluir que el algoritmo de Baeza-Yates con búsqueda binaria (BY-Binary) se destaca como el más eficiente en la mayoría de los escenarios. Ofrece el mejor rendimiento tanto en tiempo de ejecución como en número de comparaciones, especialmente cuando el número de listas a intersectar y su longitud aumentan.
El algoritmo de Melding es simple de implementar, pero su eficiencia se degrada significativamente a medida que aumenta el número de listas y su longitud. Por lo tanto, no se recomienda para conjuntos de datos grandes o con muchas listas.
El algoritmo de Babay y Kenyon esta diseñado específicamente para la intersección de múltiples listas ordenadas. Su rendimiento es aceptable en los conjuntos B y C, pero no es el más eficiente, a causa de que es el algoritmo más costoso en términos de tiempo de ejecución y número de comparaciones en todos los conjuntos de datos.
En resumen, el algoritmo de Baeza-Yates con búsqueda binaria (BY-Binary) se presenta como la mejor opción general para la intersección de listas ordenadas, ofreciendo el mejor equilibrio entre tiempo de ejecución y número de comparaciones en los conjuntos de datos probados.
En el bloque de código que se muestra a continuación, se muestra parcialmente la salida obtenida del programa en donde se puede observar que algoritmo ha sido el más rápido, el más lento y los algoritmos con las intersecciones más largas y cortas.
Análisis comparativo para Conjunto A:
El algoritmo más rápido es: BY-B1
El algoritmo más lento es: BK
El algoritmo con la interseccion mas larga es: BK
El algoritmo con la interseccion mas corta es: BY-B1
Análisis comparativo para Conjunto B:
El algoritmo más rápido es: BY-Binary
El algoritmo más lento es: BK
El algoritmo con la interseccion mas larga es: BY-Binary
El algoritmo con la interseccion mas corta es: Melding
Análisis comparativo para Conjunto C:
El algoritmo más rápido es: BY-B1
El algoritmo más lento es: BK
El algoritmo con la interseccion mas larga es: BY-Binary
El algoritmo con la interseccion mas corta es: Melding
Referencias.
Baeza-Yates, R. A., & Perleberg, C. (1992). Fast and practical algorithm for string matching. Information Processing Letters, 37(1), 13-18.
Barbay, J., & Kenyon, C. (2002). Intersecting many sorted sequences. Journal of Algorithms, 45(1), 91-112.
Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2022). Introduction to algorithms (4th ed.). MIT press.
Python Document, (2025). gzip — Soporte para archivos gzip - 3.8.20. Python.org. R Consultado el 18 de mayo de 2025, disponible en https://docs.python.org/es/3.8/library/gzip.html
Knuth, D. E. (1998). The art of computer programming, Volume 3: Sorting and searching (2nd ed.). Addison-Wesley. Consultado el 18 de mayo de 2025, disponible en https://seriouscomputerist.atariverse.com/media/pdf/book/Art%20of%20Computer%20Programming%20-%20Volume%203%20(Sorting%20&%20Searching).pdf
Zobel, J., & Moffat, A. (2006). Inverted files for text search engines. ACM Computing Surveys (CSUR), 38(2), 6.